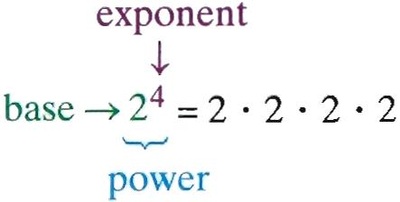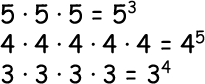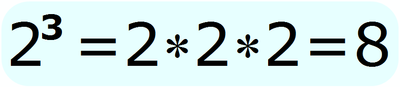Fractions, Decimals, Percents, and Exponents
Fraction Operations
Adding Fractions: When adding fractions it is important to have a common denominator for the set of fractions. A denominator is the number on the bottom of the fraction. To find a common denominator find the LCM of the denominators. The LCM will be your new denominator. Divide the LCM by the old denominator, then multiply by the old numerator (top number in the fraction). This result is your new numerator. Make sure to do this with each of the fractions. Then add the numerators, but leave the denominator the same.
Subtracting Fractions: We use the same process for subtracting fractions that we used for adding fractions, except in the last step we subtract the numerators instead of adding them.
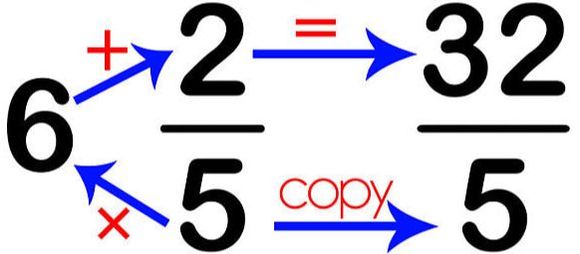
Changing a Mixed Number into an Improper Fraction: You will need to know how to change a mixed number into an improper fraction in order to multiply and divide the fractions. The way you do this is to multiply the denominator by the Whole number, then add the numerator. This result is the new numerator. The new fraction will have the same denominator.
Dividing Fractions: A division problem can be thought of as a number being "cut" into pieces. The dividend is being cut into the number of pieces determined by the divisor. The result is called the quotient. Whoa! That's alot to think about. Let's break it down... Get it... Break it down... It's Division! Okay, Never Mind.
There are a few ways to divide fractions. The most common way is to multiply the first fraction by the reciprocal of the second fraction (Keep the first fraction the same - Change to multiplication - Flip the second fraction).
Multiplying Fractions: This one is Easy Cheesy- Lemon Squeezy! All you do is multiply straight across (top x top) and (bottom x bottom). You may have to reduce after multiplying.
Adding Fractions: When adding fractions it is important to have a common denominator for the set of fractions. A denominator is the number on the bottom of the fraction. To find a common denominator find the LCM of the denominators. The LCM will be your new denominator. Divide the LCM by the old denominator, then multiply by the old numerator (top number in the fraction). This result is your new numerator. Make sure to do this with each of the fractions. Then add the numerators, but leave the denominator the same.
Subtracting Fractions: We use the same process for subtracting fractions that we used for adding fractions, except in the last step we subtract the numerators instead of adding them.
Changing a Mixed Number into an Improper Fraction: You will need to know how to change a mixed number into an improper fraction in order to multiply and divide the fractions. The way you do this is to multiply the denominator by the Whole number, then add the numerator. This result is the new numerator. The new fraction will have the same denominator.
Dividing Fractions: A division problem can be thought of as a number being "cut" into pieces. The dividend is being cut into the number of pieces determined by the divisor. The result is called the quotient. Whoa! That's alot to think about. Let's break it down... Get it... Break it down... It's Division! Okay, Never Mind.
There are a few ways to divide fractions. The most common way is to multiply the first fraction by the reciprocal of the second fraction (Keep the first fraction the same - Change to multiplication - Flip the second fraction).
Multiplying Fractions: This one is Easy Cheesy- Lemon Squeezy! All you do is multiply straight across (top x top) and (bottom x bottom). You may have to reduce after multiplying.
Addition of Multi-Digit Numbers
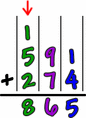
When adding numbers with more than one digit, it is important to line up the place values of the numbers. Then add starting with the last place value. Remember to carry into the next place value.
With Decimals
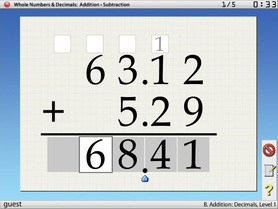
Line up the decimals then add the same way. The answer will have a decimal in the same location.
When adding numbers with more than one digit, it is important to line up the place values of the numbers. Then add starting with the last place value. Remember to carry into the next place value.
With Decimals
Line up the decimals then add the same way. The answer will have a decimal in the same location.
Subtraction of Multi-Digit Numbers & Decimals
Line up the decimals then subtract starting with the last place value. You may need to borrow from the next place value. Remember that when you borrow, you are borrowing 10, not just 1.
Line up the decimals then subtract starting with the last place value. You may need to borrow from the next place value. Remember that when you borrow, you are borrowing 10, not just 1.
Multiplication of Multi-Digit Numbers & Decimals
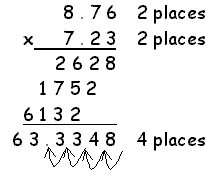
In order to multiply numbers with more than one digit begin by multiplying the last digit in each number. Carry over any answer that has more than one digit. This carried over amount will be added to the next product in line. Make sure to use a zero as a place holder. If your numbers have decimals, add up the decimal places for all the numbers. After finishing the multiplication, add the columns. The decimal will be placed into the answer the same number of times that you counted.
In order to multiply numbers with more than one digit begin by multiplying the last digit in each number. Carry over any answer that has more than one digit. This carried over amount will be added to the next product in line. Make sure to use a zero as a place holder. If your numbers have decimals, add up the decimal places for all the numbers. After finishing the multiplication, add the columns. The decimal will be placed into the answer the same number of times that you counted.
Division of Multi-Digit Numbers
Dividing numbers that have decimals is done by getting rid of the decimal in the divisor (outside of symbol). To get rid of the decimal, move the decimal to the end of the number. Now move the decimal in the dividend (under the symbol) the same number of times. You may have to add some zeroes to the end of the number to make this possible. Then divide as usual.
Dividing numbers that have decimals is done by getting rid of the decimal in the divisor (outside of symbol). To get rid of the decimal, move the decimal to the end of the number. Now move the decimal in the dividend (under the symbol) the same number of times. You may have to add some zeroes to the end of the number to make this possible. Then divide as usual.
Fractions to Decimals
To change a Fraction to a Decimal, you divide the numerator by the denominator.
Decimal to Fraction
To change a Decimal to a Fraction, consider the place value of last digit of the decimal. This will be your denominator.
|
|
|
Fraction to Percent
In order to change a fraction to a percent, find an equivalent fraction that has a denominator of 100. The numerator will be your percent. If there is no equivalent fraction with a denominator of 100, then cross multiply and divide to find the percent.
Decimal to Percent
In order to change a decimal to a percent, multiply by 100, or move the decimal 2 places to the right.
To change a percent to a decimal, divide by 100, or move the decimal 2 places to the left.
To change a percent to a decimal, divide by 100, or move the decimal 2 places to the left.

Exponents
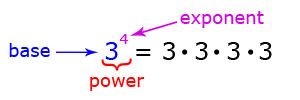
There are two parts to a number with an exponent. The big number is called the "Base". This is the number that will be multiplied. The smaller number that is lifted up is the "Exponent or Power". The Power tells us how many times to write the base. Then we multiply. This example would be "4 raised to the power of 3". As you can see, 4 is written 3 times. Then 4 is multiplied. So 4 raised to the power of 3 = 64.
There are a few different ways to write numbers with exponents.
Exponential Form is when the number is written with a base and a power.
Expanded Form is when the number is written out using multiplication.
Standard Form is the answer after the number has been multiplied.
There are two parts to a number with an exponent. The big number is called the "Base". This is the number that will be multiplied. The smaller number that is lifted up is the "Exponent or Power". The Power tells us how many times to write the base. Then we multiply. This example would be "4 raised to the power of 3". As you can see, 4 is written 3 times. Then 4 is multiplied. So 4 raised to the power of 3 = 64.
There are a few different ways to write numbers with exponents.
Exponential Form is when the number is written with a base and a power.
Expanded Form is when the number is written out using multiplication.
Standard Form is the answer after the number has been multiplied.