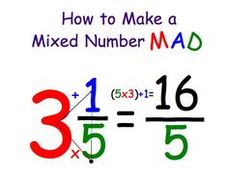Number System
Prime Numbers
*Are numbers that cannot be divided evenly by any other number than the number 1. Examples: 2, 3, 5, 7, 11, & 13 are all Prime numbers. Not all prime numbers are odd and not all odd numbers are prime.
Composite Numbers
*Are numbers that CAN be evenly divided by another number other than the number 1. Examples: 4, 6, 8, 9, 10, 12, and 14 are all Composite numbers.
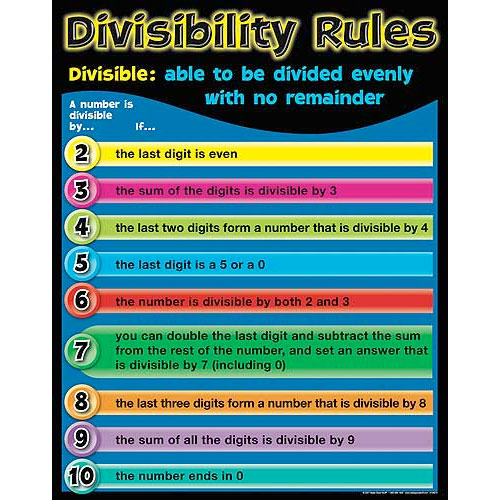
Divisibility Rules are shortcuts to find out if the number can be divided evenly by another number without having to do the whole division problem each time. If you learn and use these rules you will save yourself time in all areas of math.
*Are numbers that cannot be divided evenly by any other number than the number 1. Examples: 2, 3, 5, 7, 11, & 13 are all Prime numbers. Not all prime numbers are odd and not all odd numbers are prime.
Composite Numbers
*Are numbers that CAN be evenly divided by another number other than the number 1. Examples: 4, 6, 8, 9, 10, 12, and 14 are all Composite numbers.
Divisibility Rules are shortcuts to find out if the number can be divided evenly by another number without having to do the whole division problem each time. If you learn and use these rules you will save yourself time in all areas of math.
Greatest Common Factor
*Code Name - GCF
* The GREATEST (biggest) factor that is shared by a set of numbers.
* We find this by listing the factors of each number in the set and then comparing.
*In class, we have learned the Ladder Method. Here is a video explaining this method.
*Code Name - GCF
* The GREATEST (biggest) factor that is shared by a set of numbers.
* We find this by listing the factors of each number in the set and then comparing.
*In class, we have learned the Ladder Method. Here is a video explaining this method.
*Another method is to use the "Factor Tree" and then list each of the factors. After listing, compare what is in common. Then multiply the factors that are in common with each of the numbers in the set. (Tip: Only the factors that EVERY number in the set has in common gets multiplied). This result is the GCF!
Example: 10 is the GCF of 20 and 35 because 10 is the largest factor that is shared by 20 and 35.
Example: 10 is the GCF of 20 and 35 because 10 is the largest factor that is shared by 20 and 35.
Least Common Multiple
+Code Name: LCM
+The Least Common Multiple is the SMALLEST Multiple of a set of numbers.
+ A Multiple is a number that contains another number an integral number of times without a remainder: 12 is a multiple of 3.
+ A method of finding the LCM is to list the multiples of each number in the set and compare. The largest multiple that is shared by EVERY number in the set is the LCM.
+Code Name: LCM
+The Least Common Multiple is the SMALLEST Multiple of a set of numbers.
+ A Multiple is a number that contains another number an integral number of times without a remainder: 12 is a multiple of 3.
+ A method of finding the LCM is to list the multiples of each number in the set and compare. The largest multiple that is shared by EVERY number in the set is the LCM.
|
|
|
Distributive Property using GCF
We can rewrite an addition problem as the sum of two numbers with their greatest common factor as a common multiplier. It sounds way more confusing than it really is.
How do you do it? Start with an addition problem like Somenumber + Someothernumber = ?
Find the GCF of the set of numbers in the problem. This GCF will be the number on the outside of the parenthesis of the new expression. Next, use the quotient of the GCF and the original number as the number on the inside of the parenthesis. Do this for each of the original numbers. Your new expression should look like ////// TheGCF ( somenewnumber + someothernewnumber ) .
Click on the following link to watch the Learnzillion Video! https://learnzillion.com/assignments/V5K9APG
We can rewrite an addition problem as the sum of two numbers with their greatest common factor as a common multiplier. It sounds way more confusing than it really is.
How do you do it? Start with an addition problem like Somenumber + Someothernumber = ?
Find the GCF of the set of numbers in the problem. This GCF will be the number on the outside of the parenthesis of the new expression. Next, use the quotient of the GCF and the original number as the number on the inside of the parenthesis. Do this for each of the original numbers. Your new expression should look like ////// TheGCF ( somenewnumber + someothernewnumber ) .
Click on the following link to watch the Learnzillion Video! https://learnzillion.com/assignments/V5K9APG
|
|
|
Fraction Operations
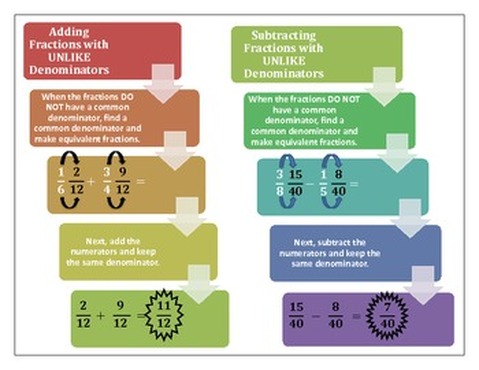
Adding Fractions: When adding fractions it is important to have a common denominator for the set of fractions. A denominator is the number on the bottom of the fraction. To find a common denominator find the LCM of the denominators. The LCM will be your new denominator. Divide the LCM by the old denominator, then multiply by the old numerator (top number in the fraction). This result is your new numerator. Make sure to do this with each of the fractions. Then add the numerators, but leave the denominator the same.
Subtracting Fractions: We use the same process for subtracting fractions that we used for adding fractions, except in the last step we subtract the numerators instead of adding them.
Changing a Mixed Number into an Improper Fraction: You will need to know how to change a mixed number into an improper fraction in order to multiply and divide the fractions. The way you do this is to multiply the denominator by the Whole number, then add the numerator. This result is the new numerator. The new fraction will have the same denominator.
Adding Fractions: When adding fractions it is important to have a common denominator for the set of fractions. A denominator is the number on the bottom of the fraction. To find a common denominator find the LCM of the denominators. The LCM will be your new denominator. Divide the LCM by the old denominator, then multiply by the old numerator (top number in the fraction). This result is your new numerator. Make sure to do this with each of the fractions. Then add the numerators, but leave the denominator the same.
Subtracting Fractions: We use the same process for subtracting fractions that we used for adding fractions, except in the last step we subtract the numerators instead of adding them.
Changing a Mixed Number into an Improper Fraction: You will need to know how to change a mixed number into an improper fraction in order to multiply and divide the fractions. The way you do this is to multiply the denominator by the Whole number, then add the numerator. This result is the new numerator. The new fraction will have the same denominator.
|
|
|